Time Complexity Of Algorithms
Generally, there is more than one method to find a solution for a particular problem. To analyze which method is the best, we check the time complexity of each method. One of the methods will consider as best which has minimum time complexity. That’s why the Time complexity is considered very useful for algorithm analysis.
Definition: The amount of time taken by an algorithm to solve a problem is called the time complexity of that algorithm. The execution time of an algorithm is totally independent of the machine execution of that code.
Classes of Time Complexity
Some classes of time complexity are discussed below, which helps us to calculate the time complexity of any algorithm
1. Constant Time Complexity – O(1)
When the number of operations does not depend on the size of the input then it will be Constant time complexity. Each statement will execute a constant number of times (i.e. 10, 100, etc).
Example: Best time complexity of Binary Search
2. Logarithmic Time Complexity – O(log n)
In the case when algorithms divide the inputs into multiples part every time then it will be logarithmic time complexity.
Example: Average time complexity of binary search algorithm is O(log n)
Note: O (nlog n) is also a logarithmic time complexity but higher value than O(log n).
3. Square Root Time Complexity –O(sqrt(n))
In the case when the algorithm requires O(N^(1/2)) evaluations, where N is input size. divide the inputs into multiples part every time then it will be logarithmic time complexity.
Example: Grover’s algorithm
4. Linear Time Complexity – O(n)
When the complexity is directly proportional to the size of the input size then it will be linear time complexity.
Example: Average time complexity of Binary Search
5. Linear Logarithmic Time Complexity – O(nlog n)
When the complexity is directly proportional to the nlogn then it will be linear logrithic time complexity.
Example: Average time complexity of Binary Search
6. Quadratic Time Complexity – O (n^2)
When the complexity is directly proportional to the squared size of the input data set then it will be quadratic time complexity.
Example: Best time complexity of Selection Sort
7. Cubic Time Complexity – O(n^3)
When the complexity is directly proportional to the cubic size of the input data set then it will be cubic time complexity.
Example: The Floyd-Warshall algorithm solves the All Pairs Shortest Paths problem. Its time complexity is O(n^3)
8. Exponential Time Complexity – O (2^n)
In the case when an input unit increases by 1, it causes you to double the number of operations performed then it will be exponential time complexity.
Example: The time complexity of the program to find all subsets by backtracking is O (2^n).
Note: O (3^n), O (4^n) is also an Exponential time complexity but higher value than O (2^n).
9. Factorial Time Complexity – O(n!)
It increases in proportion to all the products of all numbers included (e.g., 1*2*3…. ).
10. N Power N Time Complexity – O(n^n)
N^N is the highest time complexity among the others. It grows faster than n!, Since the base grows as n increases.
Time Complexity In Increasing Order
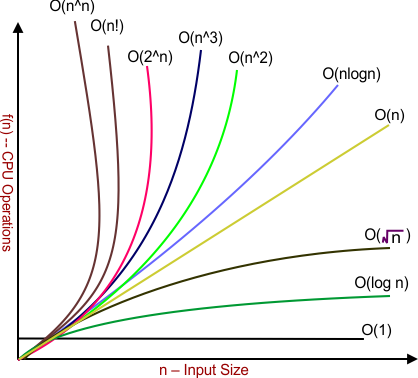
As we already discussed in this lecture, the time complexity is lowest for the constant class and highest for N^N time complexity.

Proof: We consider some parameters (i.e. Logn, n, n2, nn). Note that as we increase the value of “n” the values of parameters change according to the above-given sequence.
The following figure will explain all when the value of n=1,2,3,4……
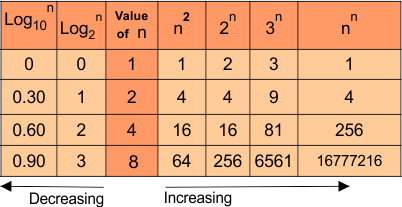
Note: For very smaller values of “n”, the given sequence may not work properly but for higher values of “n” the above sequence works 100%.
Time Complexity Table
The time complexity table of various algorithms is given below

Notations for Time Complexity
There are various types of time complexity notations, discussed under
- Big-Oh: it tells the maximum time an algorithm takes, denoted by a symbol “O”
- Big-Omega: it tells the minimum time an algorithm takes, denoted by a symbol “Ω ”
- Theta: it tells the average time an algorithm takes, denoted by a symbol “Θ”
- Small-O: almost similar to Big-Oh
- Small-Omega: almost similar to Small-Omega
Big-O Time Complexity Graph
Big-O time complexity graph for all classes of time complexity is given under