Asymptotic Notations of Algorithm
Asymptotic notations are mathematical notations used to describe the time complexity of algorithms. Asymptotic notations help to measure the efficiency of the algorithm which depends on CPU time, storage space, and other resources required for execution. The study of efficiency measurement of algorithms is called asymptotic analysis.
There are three major types of asymptotic notations to represent the time complexity of the algorithms given below.

1. Big-Oh Notation (O-Notation)
Big-O notation represents the upper bound (at most) of the running time of an algorithm. Thus, it presents the worst-case time (maximum time an algorithm takes) complexity of an algorithm.
It is a widely used notation as compared to others notations. The reason is, if we know the worst-case value for any algorithm then the average and best may guess easily. For example, if a book has 100 pages and applies a linear sort to find a particular topic, then Big-O tells the particular topic is exist on the last page (100). It is the worse case.
Let’s see the proper definition in mathematical form
If F(n) and g(n) be two non-negative functions then there exist the following rules
- n0>0, n0 is the lowest value of n in the equation
- C>0, C is constant
- f(n) ≤ c.g(n), ∀ n ≥ n0
Then f(n) = O(c.g(n))
Graphical Notation is given under
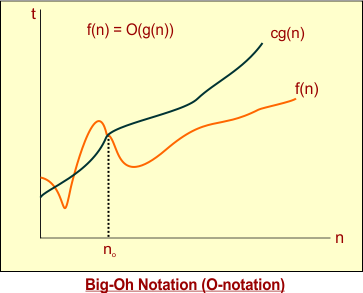
The graph of Big-Oh, as mentioned above, shows
- n is the input size in the x-axis
- t is time in the y-axis
- f(n) is a function for a particular problem that is always given.
- g(n) is the notation of Big-Oh, where c is constant and g(n) is the Big-Oh function.
Examples Of Big-Oh Notation
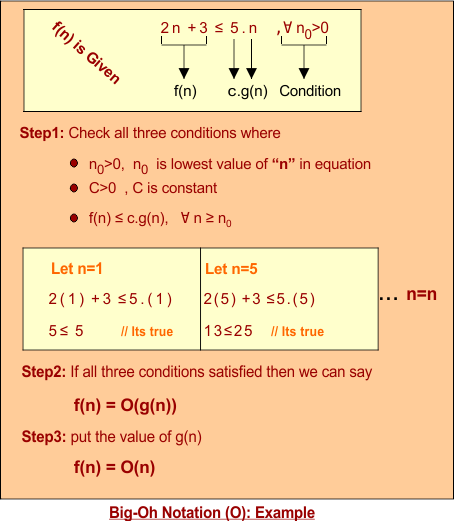
Example 01: If we want to represent given function f (n) = 2n +3 in terms of Big-O [c.g(n)] then
Tip1: If function is f(n) = 4n2 + nlogn+ 3n + 5 then g(n) will be “n2” with some constant. As “n2” is a higher degree of given function f(n) and constant “C” will be 13 “(4+1+3+5)” because of adding all constants of f(n).
|
Solution: Solution of Example 1 is explained in the following figure
Example 02: If we want to represent a given function [f (n) = 5n2 +2n +1] in terms of Big-O [c.g(n)] then
- 5n2 +2n +1 ≤ cn2 // purpose of selecting “n2” of “g(n)” means always choose the closet upper bound to satisfy the equation
- 5n2 +2n + 1 ≤ 8n2 // count all constants from the “f(n)” equation and place with a value of c, to satisfy the equation
- For n ≥ n0, Put different n values and check the results, results will be according to the given rules of Big – Oh.
For n=1,
- 5(1)2 +2(1) +1 ≤ 8(1)2
- 8 ≤8 // its true
For n=2,
- 5(2)2 +2(2) +1 ≤ 8(2)2
- 25 ≤32 // its true
Hence, it proves For all values of n, where n ≥ n0, the results are true
F(n) = 5n2 +2n +1, c=8, g(n) = n2
As F(n) = O(g(n)) So, F(n) = O(n2)
2. Omega Notation (Ω-Notation)
Omega notation represents the lower bound (at least) of the running time of an algorithm. So, it provides the best case time (minimum time an algorithm takes) complexity of an algorithm.
For example, if a book has 100 pages and applies a linear sort to find a particular topic, then Big-Omega tells the particular topic is exist at first page (1). It is best case.
Let’s look at the proper definition
Let F(n) and g(n) be two non-negative functions then there exist the following rules
- n0>0
- C>0
- F(n) ≥g(n), ∀ n ≥ n0
Then f(n) = Ω(C.g(n))
Graphical Notation is given under

Examples Of Omega Notation
Example 01: If we want to represent given function f (n) = 2n +3 in terms of Big-Omega [c.g(n)] then
- 2n +3 ≥ c.n // purpose of selecting “n” of “g(n)” means always choose the closet lower bound to satisfy the equation
- 2n +3 ≥ 1n // put constant C=1 to satisfy equation
- For all n ≥ n0 // Put different values of n and check the results, results will be according to given rules of Big – Omega as given under
| Important: Above example will also be true for all those values of function g(n) which are less than “n” (i.e. 1, nlogn etc). So, function time complexity will be (O(1), … O(nlogn)). But we choose the lower-bound value closest to the given function. |
Solution: Solution of Example 1 is explained in the following figure

Example 02:If we want to represent given function [f (n) = 2n2 +n] in terms of Big-O [c.g(n)] then
- 2n2 +n ≥ cn2 // purpose of selecting “n2” of “g(n)” means always choose the closet lower bound to satisfy the equation
- 2n2 +n ≥ 1n2 // put “C=1” to satisfy the equation
- For n ≥ n0 // Put different n values and check the results, results will be according to the given rules of Big – Oh.
For n=1,
- 2(1)2 +1 ≥ 1(1)2
- 3 ≥ 1 // its true
For n=2,
- 2(2)2 +1 ≥ 1(2)2
- 9 ≥ 4 // its true
Hence, it proves For all values of n, where n ≥ n0, the results are true
F(n) = 2n2 +n, c=1, g(n) = n2
So,
- F(n) = Ω (g(n))
- F(n) = Ω (n2)
3. Theta Notation (Θ-Notation)
Theta notation represents the upper and lower bound of the running time of an algorithm. It calculates the average-case time complexity of an algorithm.
For example, if a book has 100 pages and applies a linear sort to find a particular topic, Theta tells the particular topic is exist on the last page (50). It is an average case.
Let’s see the proper definition
Let F(n) and g(n) be two non-negative functions then there exist the following rules
- n0>0
- C1>0, C2>0,
- C2.g(n) ≤ f(n) ≤ C1.g(n), ∀ n ≥ n0
Then f(n) = Θ (g(n))
Note: if you notice, then you find that C1.g(n) is Big-Oh and C2.g(n) is Big-omega.
Graphical Notation is given under

F(n) always lies between Big-Oh and omega
Examples Of Theta Notation
Example 01: If we want to represent a given function f (n) = 2n +3 in terms of Theta then
We know, C2.g(n) ≤ f(n) ≤ C1.g(n) where C1.g(n) is Big-Oh an C2.g(n) is Big-omega

If C1.g (n) and C2.g (n) hold the same degree value, then theta function exists. We can represent average time complexity as follows
f(n) = Θ (n)
Example 02: Quadratic logarithmic time complexity function is explained in the following figure

| Note: it is also possible that Big-Oh and Big-omega hold but both have a different degree of time complexity, then theta function time complexity does not exist, as in example 3 |
Example 03:If we want to represent given function [ f(n) = n!] in terms of Theta then

Note that, Big-Oh and Big-omega hold but have different degree results. So, theta function time complexity does not exist.
Small-O and Small-Omega Notations
There are two more notations are also used which are small-O and Small-Omega
4. Small –O
It is also called little-O. Little-O is similar to Big-O except for the following two factors
- It does not use the equal sign in equation. As it use f(n) < cg(n) instead of f(n) ≤ cg(n)
- It uses any upper-bound (not closet) value that cannot be tight as in Big-O.
5. Small – Omega
It is also called little- Omega. Little – Omega is just similar to Big- Omega except for the following two factors
- It does not use equal sign in equation. As it use f(n) > cg(n) instead of f(n) ≥ cg(n)
- It uses the any lower-bound (not closet) value that cannot be tight as in Big-Omega.













